Autothrottle Landing

They need to let the autothrottles do their job and flare the aircraft not to level flight, but to a slight descent. The landing will be predictably on speed and in the touchdown zone. As a bonus, the landing will be perceived in back as a smooth one.

What follows is some geometry to explain what these pilots are doing wrong, and some physics to prove the "airspeed bleeds in the flare rotation" argument.

Of course there is an easier way. Just fly the aircraft on a 3° glide path all the way down to flare height, perform a normal flare, and look at your airspeed indicator.

1 — The objective: trade airspeed for reduced sink

2 — An example in a G450

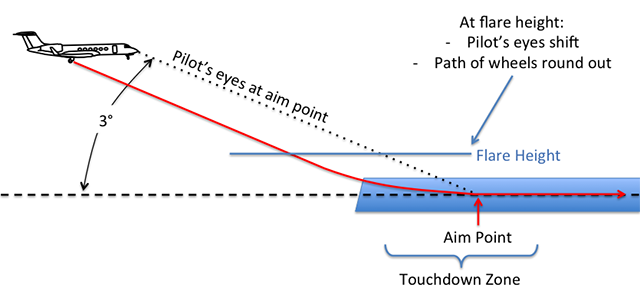
How it should look

Prior to initiating the flare, the pilot's eyes attempt to keep the runway aim point stationary on the windshield. If the pilot does not flare, his eyes will impact the runway at that point, normally 1,000' down the runway. Because most aircraft make this approach with a positive deck angle, the wheels do not simply touchdown at their actual distance behind the pilot, but at around seven times that distance. This seems counter intuitive, but the math is explained at Deck Angle.

A G450, for example, approaches with a 5° nose high attitude on a 3° glide path. Even though the wheels are only 35 feet behind the pilot's eyes, they will touchdown 275 feet behind the aim point if the pilot does not flare.

But the pilot does flare and the round out should carry the wheels to the aim point. We practice to make this happen. The force of the engines and of gravity are driving the airplane down and forward. When you rotate the nose up for the flare, some of the energy that was used to propel the airplane forward is now used to further arrest the force of gravity. You have less force available for forward motion, your speed necessarily decreases. (I prove this mathematically below, under the example.)

If you do everything right, your wheels touchdown at your aim point and you bleed off the necessary amount of speed. And you did all of that without chopping the power violently at a height above the flare initiation point.

Here's a demonstration. The landing was smooth, on speed, and the aircraft was in a three point attitude right at 1,000 feet.

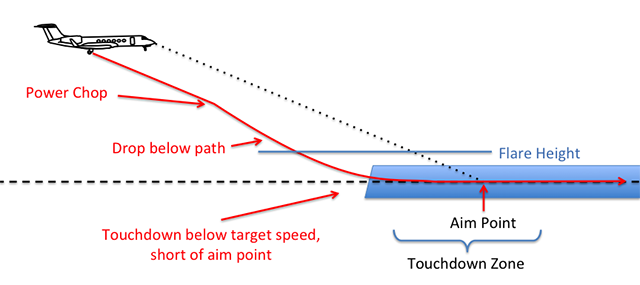
What happens when you chop the power

The primary motivation of power choppers is a misguided notion to avoid landing hot. When they chop the power well above flare height:

• The pendulum effect of the engines on most aircraft means the nose will want to pitch down. Further, the aircraft will seek its in-trim airspeed, also tending to push the nose down.
• If the pilot doesn't maintain the aim point the aircraft will fall well below the intended 3° glide path, thereby accelerating.
• The pilot has to "swap ends" at the last moment to arrest the fall.
• The end result is a low speed touchdown, short of the touchdown zone.

The technique achieves the pilot's goal of not landing too fast but risks a dangerously low speed landing as well as a landing short of the landing surface. The technique is also hard to adjust for winds.

Here's an example of what happens when you chop the power early with a headwind. Let me say that I was in the right seat with a contract pilot in the left. When he chopped the power at 150 feet I was surprised. At 100 feet we were still heading for pavement and had only lost 5 knots so I wasn't too concerned. By 50 feet we were headed for a landing in the first few hundred feet and slow, I considered calling for a go around but at that point I knew we would be on pavement, just slow. How slow? We touched down at V_REF - 20 and around 500 feet. Was he dangerously slow and short? No, not this time. But he reduced our margin of safety and I will insist he keep the autothrottles engaged next time he flies with us. Not the worst I've ever seen but certainly not something I want to do again.

We can prove you bleed the required amount of speed in the flare rotation using an example. We will use a G450:

• Landing weight: 50,000 lbs
• Environment: Sea level, 15°C, no wind
• Computed V_REF: 127 KCAS
• Approach Speed: 132 KCAS

Our objective is to touchdown at V_REF.

Because my math and physics aren't what they used to be, I am going to make an assumption here that I think is pretty close. I will use a constant thrust setting, no thrust reduction at all, to make up for ground effect. I am assuming keeping the power levers at their approach setting will give us as much speed as ground effect does. I think if I can demonstrate a speed decay under these conditions, it should also happen with the proper thrust reduction and ground effect.

We will also flare the aircraft to 200 fpm at touchdown, a firm touchdown to be sure. Since you are more likely to reduce the sink rate even more, your airspeed decay will be even greater.

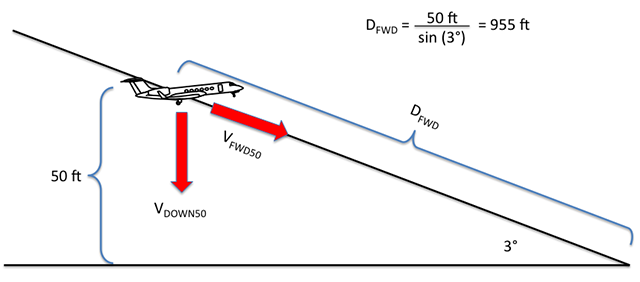
Step 1: Determine aircraft speeds and distances in the flare

$V_{\mathrm{FWD50}}=(V_{\mathrm{REF}}+5)=132$

Where V_FWD50 is our forward velocity at 50 feet. Of course it is 132 KCAS, which at sea level and 15° is equal to KTAS. We need to convert this to ft/sec, however:

$V_{\mathrm{FWD50}}=132\left(\frac{\mathrm{nm}}{\mathrm{hr}}\right)\left(\frac{6076\mathrm{ft}}{\mathrm{nm}}\right)\left(\frac{\mathrm{hr}}{3600\sec }\right)=222.8\left(\frac{\mathrm{ft}}{\sec }\right)$

With a little basic trigonometry we know the forward distance travelled as the airplane descends 50 feet:

$D_{\mathrm{FWD}}=\left(\frac{50\mathrm{ft}}{sin3}\right)=955\mathrm{ft}$

We need to compute the time required to fly this distance in order to compute the vertical velocity:

$t=\left(\frac{d}{v}\right)=\left(\frac{955\mathrm{ft}}{222.8\mathrm{ft/sec}}\right)=4.3\sec$

Computing our sink rate, V_DOWN50 is just a matter of simple division:

$V_{\mathrm{DOWN50}}=\left(\frac{d}{t}\right)=\left(\frac{50\mathrm{ft}}{4.3\sec }\right)=11.6\left(\frac{\mathrm{ft}}{\sec }\right)$

That certainly makes sense, 11.6 (ft/sec) times 60 gives us a VVI of 696 fpm, about what we would expect. Now for the sake of this example we intend to plant the airplane on the ground at 200 fpm. While the AFM recommends 360 fpm and most pilots shoot for zero, we'll do 200 for a softer touchdown. Our results will be conservative, since we will bleed less speed.

$V_{\mathrm{DOWN0}}=200\left(\frac{\mathrm{ft}}{\min }\right)\left(\frac{\min }{60\sec }\right)=3.3\left(\frac{\mathrm{ft}}{\sec }\right)$

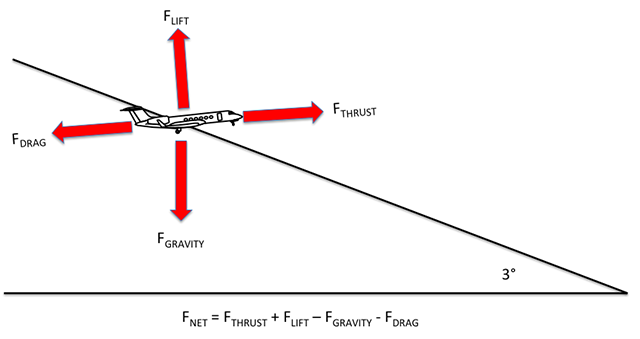
Step 2: Consider Newton's Second Law of Motion

Diagraming all the forces on the airplane at 50' will be a difficult process, but we can agree there will be a net force of some magnitude in some direction. Newton's second law of motion states:

$F=ma$

Where F = force, m = mass, and a = acceleration.

If we don't change the thrust setting we can assume the forward acceleration near 50 feet is zero. Therefore all of the acceleration at 50 feet will be vertical as we begin to arrest the sink rate:

$F_{\mathrm{NET50}}=m{\mathrm{a}}_{\mathrm{VERT50}}$

Similarly, if we consider the airplane a 0 feet to be a micron above the runway, then the vertical acceleration will have been arrested to 200 fpm and the forward acceleration will be a result of the pitch change:

$F_{\mathrm{NET0}}=m{\mathrm{a}}_{\mathrm{FWD0}}$

Since F_NET50 = F_NET0, we can say:

$m{\mathrm{a}}_{\mathrm{VERT50}}=m{\mathrm{a}}_{\mathrm{FWD0}}$

We can simplify this quite a bit by dividing the mass, m:

${\mathrm{a}}_{\mathrm{VERT50}}={\mathrm{a}}_{\mathrm{FWD0}}$

Step 3: Derive velocity from acceleration

Recall that acceleration is a change in velocity over time. For example:

$a_{\mathrm{VERT50}}=\left(\frac{V_{\mathrm{DOWN50}}-V_{\mathrm{DOWN0}}}{t}\right)$

That gives us this mess:

$\left(\frac{V_{\mathrm{DOWN50}}-V_{\mathrm{DOWN0}}}{t}\right)=\left(\frac{V_{\mathrm{FWD50}}-V_{\mathrm{FWD0}}}{t}\right)$

But if we multiply both sides of the equation by time, t, and do some addition and subtraction, we find what were looking for all along:

V_FWD0 = V_FWD50 - V_VERT50 + V_VERT0

Of course we've already solved for all of those:

$V_{\mathrm{FWD50}}=\left(\frac{222.8\mathrm{ft}}{\sec }\right)-\left(\frac{11.6\mathrm{ft}}{\sec }\right)+\left(\frac{3.3\mathrm{ft}}{\sec }\right)=214.5\left(\frac{\mathrm{ft}}{\sec }\right)$

We need to convert that to KCAS

$V_{\mathrm{FWD50}}=214.5\left(\frac{\mathrm{ft}}{\sec }\right)\left(\frac{3600\sec }{\mathrm{hr}}\right)\left(\frac{\mathrm{nm}}{6076\mathrm{ft}}\right)=127\left(\frac{\mathrm{nm}}{\mathrm{hr}}\right)$

Conclusion

We flew the approach at V_REF + 5, did not reduce thrust, and simply cut our sink rate by two-thirds. The change in energy required by the pitch change was enough to bleed the airspeed to V_REF.