As a brand new Air Force pilot in 1979, the height of my navigation skills involved holding a terrain chart in one hand while cradling the stick of a T-38 flying at "the speed of heat" 500 feet off the deck trying not to get lost. I knew what latitude and longitude meant, but they were not important in my day-to-day flying. Years later, flying in flight levels and not feet, navigating between continents and not mountains, the coordinates that pinpoint positions on the globe are important again.
— James Albright
Updated:
2016-10-23
Most of this is transparent to most pilots and navigation as a skill has become a lost art. The last cadre of truly professional air navigators cut their teeth with Air Force Manual 51-40, Air Navigation. You don't need to know about AFM 51-40, but if you really want to know what the stuff on the chart means, read on.
If you would like to know more about the history of measuring latitude and longitude — History? Yes, history. — see: Latitude & Longitude.

1
Great circle

Great circle,
(AFM 51-40, figure 2-2)
- For most navigational purposes, the earth is assumed to be a perfect sphere, although in reality it is not. Inspection of the earth's crust reveals that there is a height variation of approximately 12 miles from the top of the tallest mountain to the bottom of the deepest point in the ocean.
- Measured at the equator, the earth is approximately 6,887.91 nautical miles in diameter, while the polar diameter is approximately 6,864.57 nautical miles, and this difference may be used to express the ellipticity of the earth.
- A great circle is defined as a circle on the surface of a sphere whose center and radius are those of the sphere itself.
- The arc of a great circle is the shortest distance between two points on a sphere, just as a straight line is the shortest distance between two points on a plane.
- Circles on the surface of the sphere other than great circles may be defined as small circles. A small circle is a circle on the surface of the earth whose center and/or radius are not that of the sphere. A special set of small circles, called latitude, is discussed later.
Source: AFM 51-40, pages 2-1 to 2-2.
From a pilot's perspective, a great circle is simply the shortest route between two points on the globe.
2
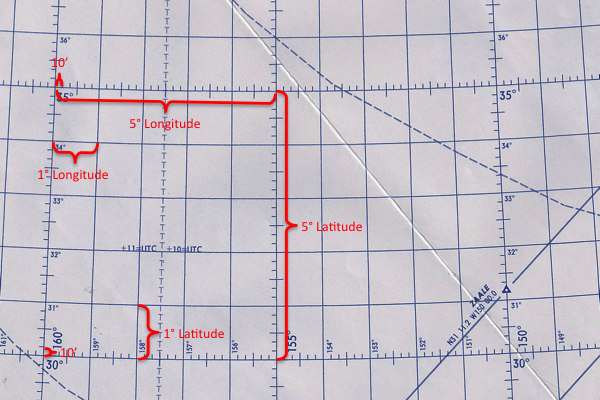
Latitude and longitude
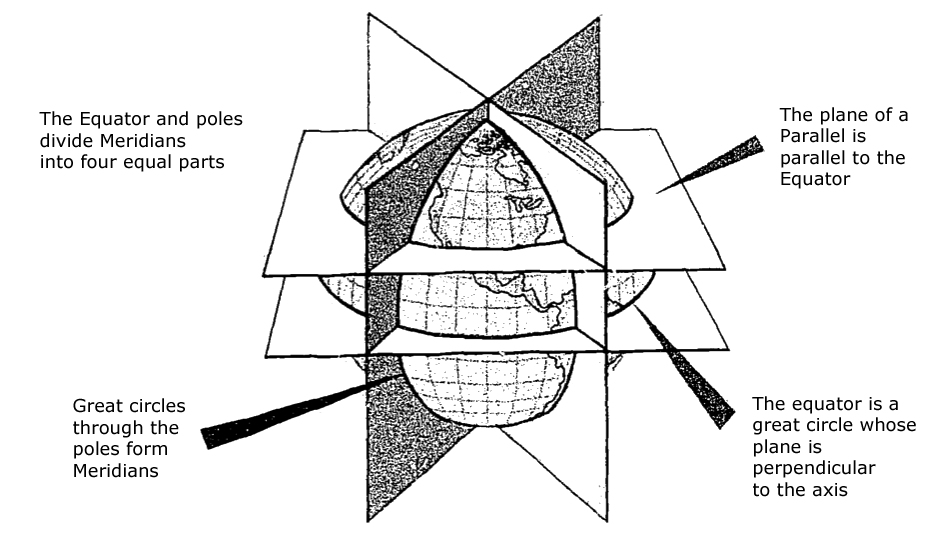
Planes of the Earth,
(AFM 51-40, figure 2-3.
- A system of coordinates has been developed to locate positions on the earth by means of imaginary reference lines. These lines are known as parallels of latitude and meridians of longitude.
- Once a day the earth rotates on its north-south axis which is terminated by the two poles.
- A great circle drawn through the poles is called a meridian, and an infinite number of great circles may be constructed in this manner. Each meridian is divided into four quadrants by the equator and the poles. Since a circle is arbitrarily divided into 360 degrees, each of these quadrants therefore contains 90 degrees.
- Take a point on one of these meridians 30 degrees north of the equator. Through this point pass a plane perpendicular to the north-south axis of rotation. This plane will be parallel to the plane of the equator [as shown in the figure] and will intersect the earth in a small circle called a parallel or parallel of latitude. The particular parallel of latitude chosen is at 30° N, and every point on this parallel will be at 30° N. In the same way, other parallels can be constructed at any desired latitude, such as 10 degrees, 40 degrees, etc.
Source: AFM 51-40, pages 2-3 to 2-4.

Longitude East and West of Greenwich Meridian,
(AFM 51-40, figure 2-5
- The latitude of a point can be shown as 20° N or 20° S of the equator, but there is no way of knowing whether one point is east or west of another. This difficulty is resolved by use of the other component of the coordinate system, longitude, which is the measurement of the east-west distance.
- There is not, as with latitude, a natural starting point for numbering, such as the equator. The solution has been to select an arbitrary starting point. A great many places have been used, but when the English speaking people began to make charts, they chose the meridian through their principal observatory in Greenwich, England, as the origin for counting longitude, and this point has been adopted by most countries of the world. This Greenwich meridian is sometimes called the prime or first meridian, though actually it is the zero meridian. Longitude is counted east and west from this meridian through 180 degrees, and shown [in the figure].
Source: AFM 51-40, pages 2-3 to 2-4.
- Latitude is expressed in degrees up to 90, and longitude is expressed in degrees up to 180. The total number of degrees in any one circle cannot exceed 360.
- A degree (°) of arc may be subdivided into smaller units by dividing each degree into 60 minutes (') of arc.
- Each minute may be further subdivided into 60 seconds (") of arc.
- Measure may also be made, if desired, in degrees, minutes, and tenths of minutes.
- A position on the surface of the earth is expressed in terms of latitude and longitude. Latitude is expressed as being either north or south of the equator, and longitude as either east or west of the prime meridian.
Source: AFM 51-40, pages 2-4 to 2-5.
3
Geographic coordinates, updated, standardized
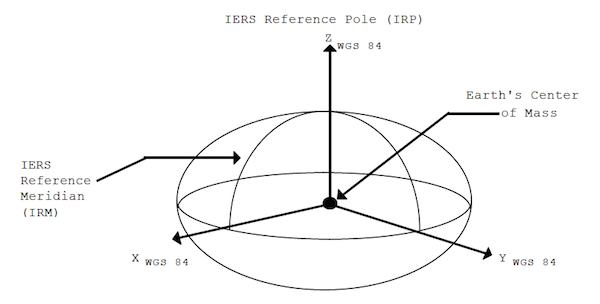
WGS84 Coordinate System Definition,
(NIMA, Figure 2.1)
The WGS 84 Coordinate System is a Conventional Terrestrial Reference System (CTRS). The definition of this coordinate system follows the criteria outlined in the International Earth Rotation Service (IERS) Technical Note 21 [1]. These criteria are repeated below:
- It is geocentric, the center of mass being defined for the whole Earth including oceans and atmosphere
- Its scale is that of the local Earth frame, in the meaning of a relativistic theory of gravitation
- Its orientation was initially given by the Bureau International de l'Heure (BIH) orientation of 1984.0
- Its time evolution in orientation will create no residual global rotation with regards to the crust
The WGS 84 Coordinate System is a right-handed, Earth-fixed orthogonal coordinate system and is graphically depicted in [the figure].
- Origin = Earth's center of mass
- Z-Axis = The direction of the IERS Reference Pole (IRP). This direction corresponds to the direction of the BIH Conventional Terrestrial Pole (CTP) (epoch 1984.0) with an uncertainty of 0.005
- X-Axis = Intersection of the IERS Reference Meridian (IRM) and the plane passing through the origin and normal to the Z-axis. The IRM is coincident with the BIH Zero Meridian (epoch 1984.0) with an uncertainty of 0.005
- Y-Axis = Completes a right-handed, Earth-Centered Earth-Fixed (ECEF) orthogonal coordinate system
Source:NIMA, ¶2.1
There is only one thing you need to know about WGS-84: your airplane uses it so the charts you use had better use it too. There are systems out there that are different enough to be critical on approach.
More about this: WGS-84.
References
(Source material)
Air Force Manual (AFM) 51-40, Air Navigation, Flying Training, 1 July 1973
World Geodetic System 1984, Department of Defense, National Imagery and Mapping Agency (NIMA), NSN 7643-01-402-0347, NIMA TR8350.2, Third Edition, Amendment 1, 3 January 2000