The U.S. Air Force used to think every pilot needs to experience supersonic flight so we all got trained in it. They no longer do that so the training was either too expensive or unnecessary. In any case, most of us are constrained with a VMO that begins with a zero so this section of Basic Aerodynamics has been pared down a bit, but it hasn't gone away.
— James Albright
Updated:
2017-12-10
You might be thinking "High Speed Flight" doesn't apply to you and that might be true. But chances are it does apply to your wings. Compressibility not only impacts the way your aircraft flies, but the way its instruments relate your airspeed and altitude measurements. Critical Mach affects most jet aircraft that fly in the transonic range and that impacts your Stability and Control, so please read on...
3 — Obtaining a higher Mach number

1
Compressibility
We amateur aerodynamacists like to blame compressibility for all sorts of ills. I hear it most often when talking about the changeover from indicated or calibrated to Mach number in a climb. I don't think that is true, but I can't prove it. So I'll just discuss what I know to be true.
Nature of Compressibility
- At low flight speeds the study of aerodynamics is greatly simplified by the fact that air may experience relatively small changes in pressure with only negligible changes in density. The airflow is termed incompressible since the air may undergo changes in pressure without apparent changes in density. Such a condition of airflow is analogous to the flow of water, hydraulic fluid, or any other incompressible fluid. However, at high flight speeds the pressure changes that take place are quite large and significant changes in air density occur. The study of airflow at high speeds must account for these changes in air density and must consider that the air is compressible and that there will be "compressibility effects."
- A factor of great importance in the study of high speed airflow is the speed of sound. The speed of sound is the rate at which small pressure disturbances will be propagated through the air and this propagation speed is solely a function of air temperature.
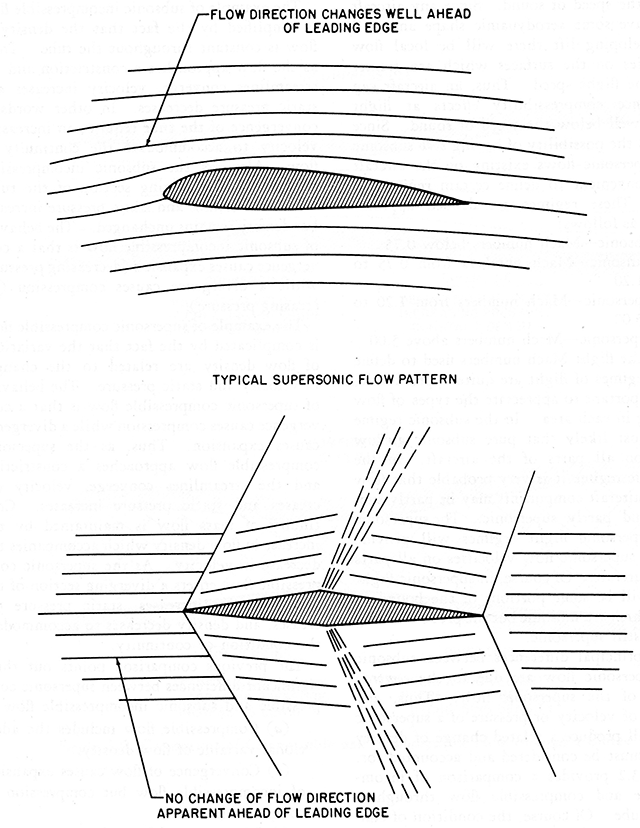
- As an object moves through the air mass, velocity and pressure changes occur which create pressure disturbances in the airflow surrounding the object. Of course, these pressure disturbances are propagated through the air at the speed of sound. If the object is traveling at low speed the pressure disturbances are propagated ahead of the object and the airflow immediately ahead of the object is influenced by the pressure field on the object. Evidence of this "pressure warning" is seen in the typical subsonic flow pattern of figure 3 where there is upwash and flow direction change well ahead of the leading edge. If the object is traveling at some speed above the speed of sound the airflow ahead will not be influenced by the pressure field on the object since pressure disturbances cannot be propagated ahead of the object. Thus as the flight speed nears the speed of sound a compression wave will form at the leading edge and all changes in velocity and pressure will take place quite sharply and suddenly.
- It is important to note that compressibility effects are not limited to flight speeds at and above the speed of sound. Since any aircraft will have some aerodynamic shape and will be developing lift there will be local flow velocities on the surfaces which are greater than flight speed. Thus, an aircraft can experience compressibility effects at flight speeds well below the speed of sound. Since there is a possibility of having both subsonic and supersonic flows existing on the aircraft it is convenient to define certain regimes of flight. These regimes are defined approximately as follows:
- Subsonic — Mach numbers below 0.75
- Transonic — Mach numbers from 0.75 to 1.20
- Supersonic — Mach number from 1.20 to 5.00
- Hypersonic — Mach numbers above 5.00
- The behavior of supersonic compressible flow is that a convergence causes compression while a divergence causes expansion. Thus, as the supersonic compressible flow approaches a constriction and the streamlines converge, velocity decreases and static pressure increases.
Source: Hurt, pp. 201-205
Compressibility Effects on Airspeed Measurement
The equivalent airspeed (EAS) is the result of correcting the (CAS) for compressibility effects. At high flight speeds the stagnation pressure recovered in the pitot tube is not representative of the airstream dynamic pressure due to a magnification by compressibility Compressibility of the airflow produces a stagnation pressure in the pitot which is greater than if the flow were incompressible. As a result, the airspeed indication is given an erroneous magnification. The standard airspeed indicator is calibrated to read correct when at standard sea level conditions and thus has a compressibility correction appropriate for these conditions.
Source: Hurt, pp. 11-12
We see that compressibility does have an impact going from CAS to EAS. But what about TAS?
- One further correction must be made to obtain true airspeed. The airspeed indicator measures dynamic pressure which is:
- As altitude increases, the density ratio σ decreases. If the airspeed indicator is calibrated for sea level density ratio, it will be in error at all altitudes where sigma is not 1.0, and it will read values that are less than the true airspeed. In some airspeed indicators there is a barometric compensating device, and true airspeed is read directly from the instrument.
- True Airspeed (TAS), coupled with ambient density ratio, produces the same dynamic pressure as EAS, coupled with standard sea level density ratio. That is:
- But σ0 = 1.0, so
Source: Dole, pp. 24-25
It is true that compressibility will have an impact on TAS, but that is because it impacted EAS first. The reason TAS varies so greatly has more to do with dynamic pressure.
2
Critical Mach
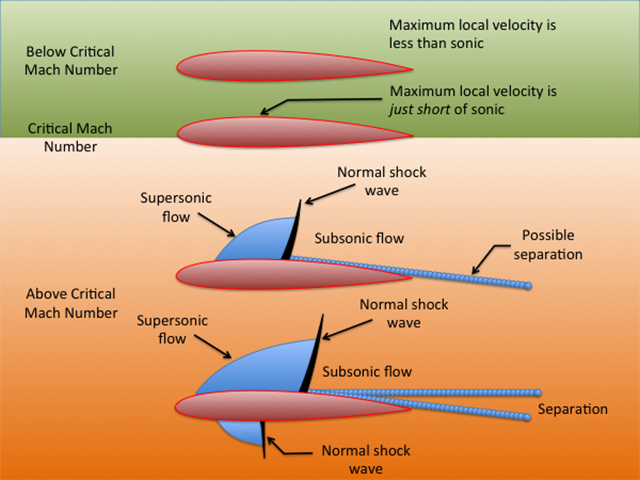
- If the flight Mach number increases, so does the local velocity on top of the wing. At some flight Mach number the local maximum velocity reaches sonic speed, M = 1.0. This flight Mach number is called the critical Mach number.
- Once MCRIT is exceeded, the aircraft is flying in the transonic speed range. Supersonic airflow exists in the area of maximum thickness on top of the wing, subsonic flow exists elsewhere.
- As the air flows through the normal shock wave it undergoes a rapid compression. The compression decreases the kinetic energy of the airstream and converts it into a pressure and temperature increase behind the shock wave. The heat rise behind the shock wave is either radiated to the atmosphere or absorbed by the wing surface, but in either case it is lost, and this lost energy must be continuously supplied by the engines. This energy loss represents a type of drag known as wave drag.
Source: Dole, p. 217
Below Critical Mach
If the speed of the air foil is such that all of the local air flow is subsonic, the air foil is said to be below its critical Mach number. The lift and drag characteristics of the airfoil are, for the most part, conventional.
At Critical Mach
At the point where the first hint of supersonic air flow occurs above the wing, the air foil is said to be at its critical Mach number. This is the last point at which air can be considered incompressible and there is no shock wave to disturb the local air flow.
Above Critical Mach
As critical Mach number is exceeded a normal shockwave forms between the boundary of supersonic and subsonic airflow. The area in front of this shockwave tends to be smooth, as the airflow has a gradual transition over the leading edge of the airfoil.
Behind the shockwave is a greatly increased static pressure, fighting to pull up the boundary layer. There is a tug of war between the kinetic energy of the air holding it to the airfoil, and the static pressure pulling it away. As the speed of the airfoil is further increased, the static pressure begins to win out and airflow separation occurs.
As a result, induced drag increases, lift decreases, and the wing may experience stability and control issues.
3
Obtaining a higher Mach number
- In order to obtain a high critical Mach number from an airfoil at some low lift coefficient the section must have:
- Low thickness ratio. The point of maximum thickness should be aft to smooth the pressure distribution.
- Low camber. The mean camber line should be shaped to help minimize the local velocity peaks.
- If supersonic flight is a possibility the thickness ratio and leading edge radius must be small to decrease wave drag.
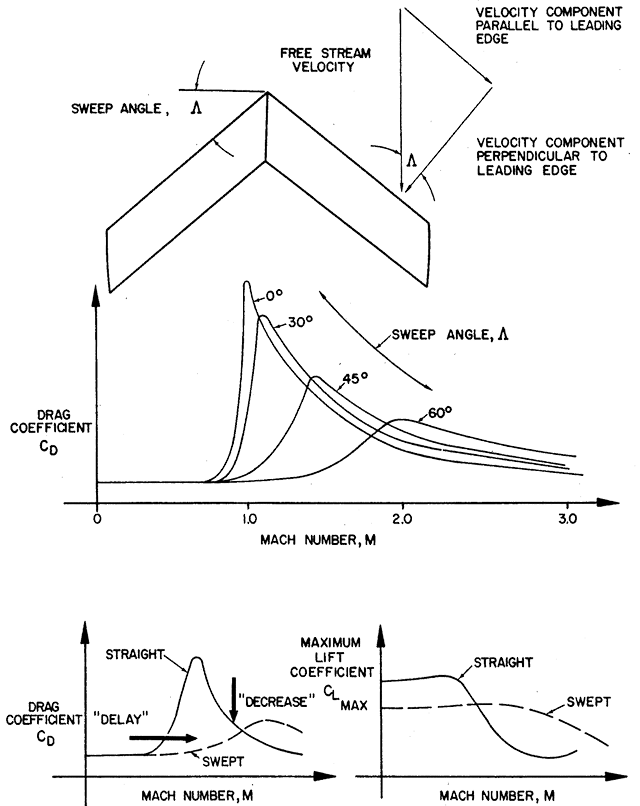
- Sweepback produces an unusual effect on the high speed characteristics of a surface and has basis in a very fundamental concept of aerodynamics. The swept wing shown has the streamwise velocity broken down to a component of velocity perpendicular to the leading edge and a component parallel to the leading edge. The component of speed perpendicular to the leading edge is less than the free stream speed (by the cosine of the sweep angle) and it is this velocity component which determines the magnitude of the pressure distribution.
- The component of speed parallel to the leading edge could be visualized as moving across constant sections and, in doing so, does not contribute to the pressure distribution on the swept wing. Hence, sweep of a surface produces a beneficial effect in high speed flight since higher flight speeds may be obtained before components of speed perpendicular to the leading edge produce critical conditions on the wing. This is one of the most important advantage of sweep since there is an increase in critical Mach number, force divergence Mach number, and the Mach number at which the drag rise will peak. In other words, sweep with delay the onset of compressibility effects.
Source: Hurt, pg. 223
4
Adjusting critical Mach with wing sweep
- A wing produces lift by accelerating the air which passes over the top surface to a higher speed than that which passes under the bottom surface. The greater the difference between these two speeds the higher to difference in pressure, hence the larger the lift vector.
- Because the local speed of the upper surface air is higher than the free stream speed — a good bit higher where the camber is marked — it is clear that this airstream will become sonic before the effect first become apparent free stream reaches the sonic value. At this speed local shock waves are formed on the wing and compressibility effects become apparent; the drag increases, buffeting is felt and changes in lift and the position of the centre of pressure occur which, at a fixed tail angle, are reflected as changes in pitch. The Mach number at which these compressibility effects first become apparent is the critical Mach number; all other parameters aside, this can be quite low for a straight wing, around 0.7 Mach number.
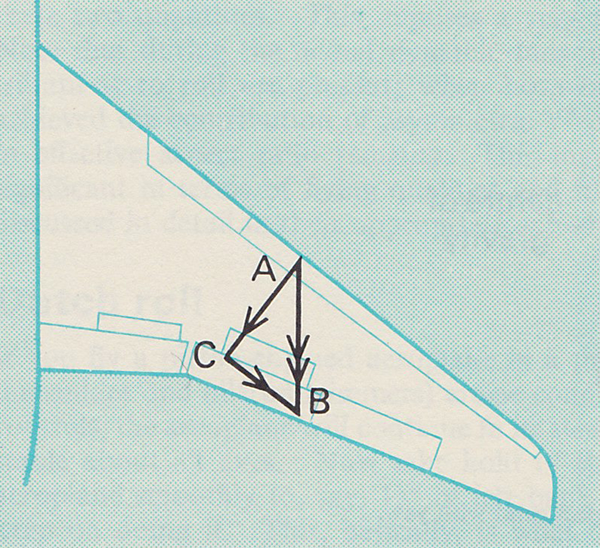
- By sweeping a wing significantly, it will be remembered, the velocity vector normal to the leading edge is made less than the chord wise resultant. In [the figure] AC is shorter than AB. As the wing is responsive only to the velocity vector normal to the leading edge, for a given Mach number the effective chord wise velocity is reduced (in effect the wing is persuaded to believe that it is flying slower than it really is). This means that the airspeed can be increased before the effective chord wise component become sonic and thus the critical Mach number is raised.
Source: Davies, pg. 96-98
See Stability and Control for more about wing sweep.
5
Mach number effect
With the advent of the big jet three things occurred to make life even more difficult. The size of the aeroplane increased enormously and, with increase altitude capability, the speed increase difficulty was compounded by Mach number effects which caused pitch changes on the aeroplane, upset the pressure distribution over the control surfaces and brought about unwanted changes in hinge moments. It was about this time that the design of the pure aerodynamic control was seen to be, perhaps not impossible, but certainly very difficult, costly and time consuming. Something was needed to remove the problems — and the answer lay in operating the control surface by pure power.
Source: Davies, pg. 24
As we've seen, the aerodynamic forces on a wing change at critical Mach. Using powered flight controls and increasing the wing sweep help, but these fixes may not be enough for some wings.
References
(Source material)
Davies, D. P., Handling the Big Jets, Civil Aviation Authority, Kingsway, London, 1985.
Dole, Charles E., Flight Theory and Aerodynamics, 1981, John Wiley & Sons, Inc, New York, NY, 1981.
Hurt, H. H., Jr., Aerodynamics for Naval Aviators, Skyhorse Publishing, Inc., New York NY, 2012.